Found 11 talks width keyword gravitation

Abstract
I present the recent results obtained using the updated version of MG-MAMPOSSt, a code that constrains modified gravity (MG) models viable at cosmological scales using determination of galaxy cluster mass profiles with kinematics and lensing analyses. I will discuss limitations and future developments of this method in view of upcoming imaging and spectroscopic surveys, as well as the possibilities of including X-ray data to break degeneracy among model parameters. Finally I will show preliminary results about the constraints that can be obtained on the inner slope of dark matter profiles when adding the velocity dispersion of the Brightest Central Galaxy (BCG) in the dataset of MG-MAMPOSSt.

Abstract
I present a detailed analysis of the scaling relations of ETGs and suggest a way to predict the evolution of the distributions of galaxies in these planes. This new approach is able to account of several features observed in the FP projections and of the tilt of the Fundamental Plane.
Abstract
Vimos Public Extragalactic Redshift Survey (VIPERS) is a spectroscopic survey designed to investigate the spatial distribution of ~90k galaxies on redshift 0.4<z<1.2. The catalogue of spectroscopic observations, combined with auxiliary photometric data, is perfect for evolutionary studies of different types of galaxies. But also for tracing rare objects. One of them are the so-called “red nuggets”, progenitors of the most massive galaxies in the local Universe. The discovery of red nuggets - highly massive, passive and extremely compact galaxies - at high redshift challenged the leading cosmological models, as they do not fit into the evolutionary paths of passive galaxies. Taking into account that the galaxies' mergers are stochastic events, it is possible that some red nuggets remain relatively unaltered for billions of years. Those survivors constitute a group of unique galaxies in the local Universe, commonly named “relics”. Despite numerous studies dedicated to red nuggets and relics, the link between the population of compact, massive, passive galaxies in the early Universe and their remnants in the local Universe, is still poorly understood.
In my talk I will present the first spectroscopically selected catalogue of red nuggets at the intermediate redshift. It is the most extensive catalogue of this kind of galaxies above redshift z > 0.5. Selected under the most strict criteria, the group of 77 objects consists of a statistically important sample, which allows for analysis of physical properties of those rare passive giants. I will discuss the influence of compactness criteria on the sample size. Moreover I will present VIPERS red nuggets number densities and discuss the environmental preferences of those exceptional galaxies.
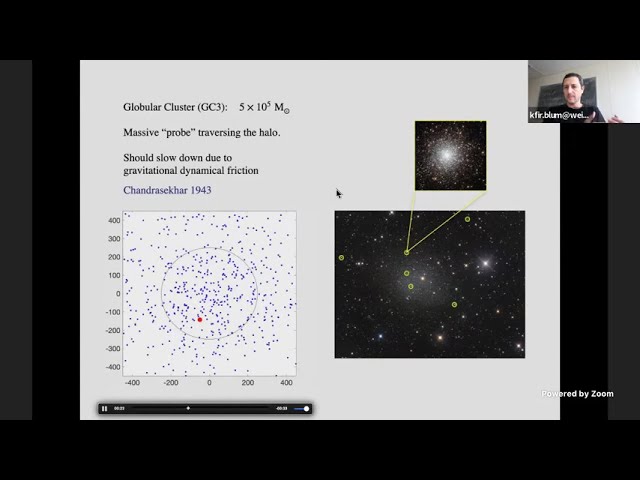
Abstract
Gravitational dynamical friction affecting the orbits of globular clusters (GCs) was studied extensively as a possible formation mechanism for nuclear star clusters in galaxies. In well-known examples that showcase this phenomenon, like the Milky Way and M31 galaxies, the medium which affects the dynamical friction is dominated by bulge stars. In comparison, the case for dynamical friction in dark matter-dominated systems is much less clear. A puzzling example is the Fornax dwarf galaxy, where the observed positions of GCs have long been suspected to pose a challenge for dark matter, dynamical friction theory, or both. We search for additional systems that are dark matter-dominated and contain a rich population of GCs, offering a test of the mechanism. A possible example is the ultra diffuse galaxy NGC5846-UDG1: we show that GC photometry in this galaxy provide evidence for the imprint of dynamical friction, visible via mass segregation. If confirmed by future analyses of more GC-rich UDG systems, these observations could provide a novel perspective on the nature of dark matter.
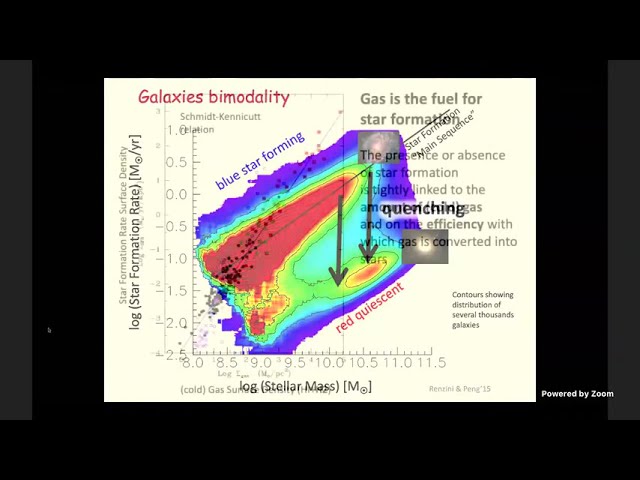
Abstract
In the local universe most of the stellar mass is in passive galaxies, where star formation is
absent or at very low levels. Understanding what are the mechanisms that have been
responsible for quenching star formation in galaxies, and transforming them into passive,
quiescent systems, is one of the main observational and theoretical challenges of extragalactic
astrophysics. I will give a brief overview of the several possible quenching causes and physical
processes that have been proposed so far, ranging from feedback from black hole accretion and
starburst activity, to effects associated with the large scale environment in which galaxies live.
Although most of these mechanisms and causes play a role in different classes of galaxies and
at different epochs, multi-band observations are providing growing evidences that just a few of
them play the key, dominant role.
I will conclude by providing prospects for further investigating these aspects and tackling open
questions with the next generation of observing facilities.

Abstract

Abstract
Bosonic ultra-light dark matter (ULDM) in the mass range m ~ $10^{-22} - 10^{-21} \rm eV$ has been invoked as a motivated candidate with new input for the small-scale `puzzles' of cold dark matter. Numerical simulations show that these models form cored density distributions at the center of galaxies ('solitons'). These works also found an empirical scaling relation between the mass of the large-scale host halo and the mass of the central soliton. We show that this relation predicts that the peak circular velocity of the outskirts of the galaxy should approximately repeat itself in the central region. Contrasting this prediction to the measured rotation curves of well-resolved near-by galaxies, we show that ULDM in the mass range m ~ $10^{-22} - 10^{-21} \rm eV$ is in tension with the data.

Abstract
Things should be made simple, but not simpler.
What we want to show is that General Relativity, as it stands today, can be considered as a gravitational theory of low velocity spinless matter, and therefore a restricted theory of gravitation.
Gravity is understood as a geometrization of spacetime. But spacetime is also the manifold of the boundary values of the spinless point particle in a variational approach. Since all known elementary matter, baryons, leptons and gauge bosons are spinning objects, it means that the manifold, which we call the kinematical space, where we play the game of the variational formalism of a classical elementary particle must be greater than spacetime.
Mathematics shows that this manifold for any arbitrary mechanical system is always a Finsler metric space, such that the variational formalism can be interpreted as a geodesic problem on this metric space.
This manifold is just the flat Minkowski space for the free spinless particle. Any interaction modifies its flat Finsler metric as gravitation does.
The same thing happens for the spinning objects, but now the Finsler metric space has more dimensions and its metric is modified by any interaction, so that to reduce gravity to the modification only of the metric of the spacetime submanifold is to make a simpler theory, the gravitational theory of spinless matter.
Even the usual assumption that the modification of the metric only produces a Riemannian metric of the spacetime is also a restriction because in general the coefficients for a Finsler metric, are also dependent on the velocities. Removal of the velocity dependence of metric coefficients is equivalent to consider the restriction to low velocity matter.
In the spirit of unification of all forces, gravity cannot produce, in principle, a different and simpler geometrization than any other interaction.
References: arXiv: 1203.4076

Abstract
Contrary to popular belief, on very large distance scales visible matter stubbornly refuses to "fall" according to the laws of gravity of both Newton and Einstein. The paradox has led to the introduction of dark matter, purporting to explain the observed surplus of gravitational pull. The logical possibility remains that there is no dark matter, what you see is all there is, and that the paradox simply signals the break down of the Einstein-Newton theory of gravity. I will review alternative theories of gravity that do away with the need for dark matter. Surprisingly Solar system gravitational experiments, such as those associated with the LISA Pathfinder mission, might settle the score between the two approaches.
Abstract
A Friedman-like cosmological model, based on noncommutative geometry, is presented. Its Planck level is totally nonlocal with no space and no time. The dynamics on this level is strongly probabilistic which makes the initial singularity statistically insignificant. Space, time and the standard dynamics emerge when one goes from the non-commutative regime (on the Planck level) to the usual "commutative physics".
« Newer 1 | 2 Older » Last >>
Upcoming talks
- Runaway O and Be stars found using Gaia DR3, new stellar bow shocks and search for binariesMar Carretero CastrilloTuesday April 30, 2024 - 12:30 GMT+1 (Aula)
- Detecting GWs in the muHz: natural and artificial satellites as GW detectorsProf. Diego BlasThursday May 2, 2024 - 10:30 GMT+1 (Aula)









